Bluetongue Virus: Thermal Performance Curves

Source: El Moustaid et al. 2021 Supplement | Data: Lysyk & Danyk 2007, Mayo et al. 2020

This analysis recreates key thermal performance curves from the Bluetongue virus transmission study, fitting Bayesian models to estimate Maximum A Posteriori (MAP) parameters for each trait. The solid lines show posterior means/medians with 95% HPD intervals (dashed lines).

Adult Mortality Rate (μ)

Temp range: 10.3–30.9 °C

mu range: 0.037–0.138  per day

Thermal Performance Curve (Quadratic via bayesTPC)

Creating NIMBLE model:
 - Configuring model.

 - Compiling model.

Creating MCMC:
 - Configuring MCMC.
 - Compiling MCMC.
 - Running MCMC.

Progress:
|-------------|-------------|-------------|-------------|
|-------------------------------------------------------|
|-------------|-------------|-------------|-------------|
|-------------------------------------------------------|
|-------------|-------------|-------------|-------------|
|-------------------------------------------------------|
|-------------|-------------|-------------|-------------|
|-------------------------------------------------------|

Configuring Output:
 - Finding Max. a Post. parameters.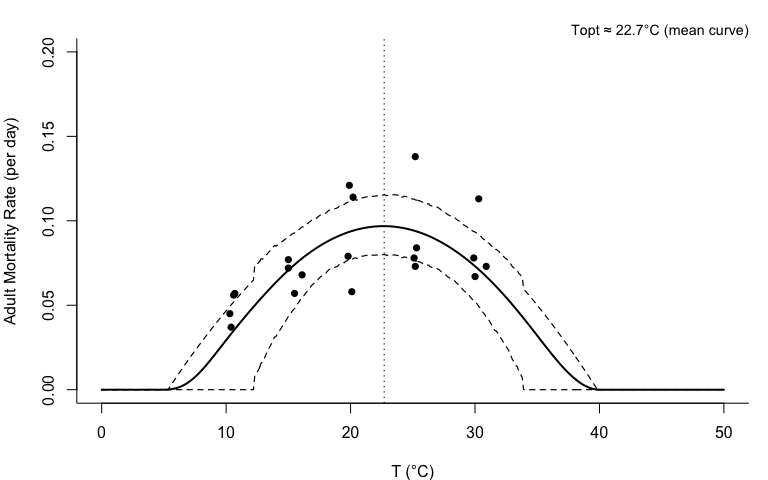

**MAP Estimates (μ):**

• T_min = 6.03 °C
• T_max = 39.97 °C
• q = 3e-04 
• sigma.sq = 4e-04 

Midge Fecundity (EFD)

Creating NIMBLE model:
 - Configuring model.

 - Compiling model.

Creating MCMC:
 - Configuring MCMC.
 - Compiling MCMC.
 - Running MCMC.

Progress:
|-------------|-------------|-------------|-------------|
|-------------------------------------------------------|
|-------------|-------------|-------------|-------------|
|-------------------------------------------------------|
|-------------|-------------|-------------|-------------|
|-------------------------------------------------------|
|-------------|-------------|-------------|-------------|
|-------------------------------------------------------|

Configuring Output:
 - Finding Max. a Post. parameters.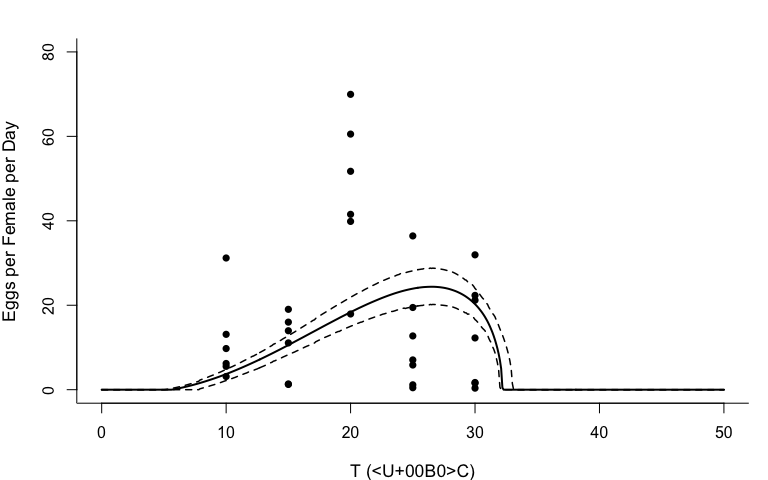

**MAP Estimates (EFD):**

• T_min = 12.9 °C

• T_max = 36 °C

• q = 0.023 

• sigma.sq = 55.7955 

Larval Survival Probability (pL)

Creating NIMBLE model:
 - Configuring model.

 - Compiling model.

Creating MCMC:
 - Configuring MCMC.
 - Compiling MCMC.
 - Running MCMC.

Progress:
|-------------|-------------|-------------|-------------|
|-------------------------------------------------------|
|-------------|-------------|-------------|-------------|
|-------------------------------------------------------|
|-------------|-------------|-------------|-------------|
|-------------------------------------------------------|
|-------------|-------------|-------------|-------------|
|-------------------------------------------------------|

Configuring Output:
 - Finding Max. a Post. parameters.

**MAP Estimates (pL):**

• T_min = 18.01 °C

• T_max = 37.24 °C

• q = 2e-04 

• sigma.sq = 0.00302 

Biting Rate (a)

Creating NIMBLE model:
 - Configuring model.

 - Compiling model.

Creating MCMC:
 - Configuring MCMC.
 - Compiling MCMC.
 - Running MCMC.

Progress:
|-------------|-------------|-------------|-------------|
|-------------------------------------------------------|
|-------------|-------------|-------------|-------------|
|-------------------------------------------------------|
|-------------|-------------|-------------|-------------|
|-------------------------------------------------------|
|-------------|-------------|-------------|-------------|
|-------------------------------------------------------|

Configuring Output:
 - Finding Max. a Post. parameters.

**MAP Estimates (a):**

• T_min = 11.4 °C

• T_max = 36 °C

• q = 4e-04 

• sigma.sq = 0.008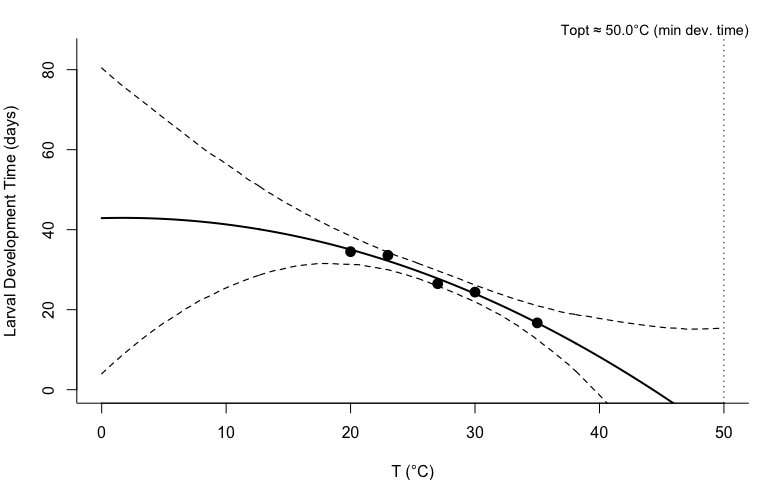 

Larva’s Development Time (LDT)

**Fitted Quadratic Model (LDT):**

• Intercept = 27.78 

• Linear coefficient = -1.2032 

• Quadratic coefficient = -0.023137 

• Residual SD = 1.42 

• R-squared = 0.981 

**Model:** LDT = 27.78 + -1.2032 *(T - 27 ) + -0.023137 *(T - 27 )²

**Note:** Development time decreases with temperature (faster development at higher T).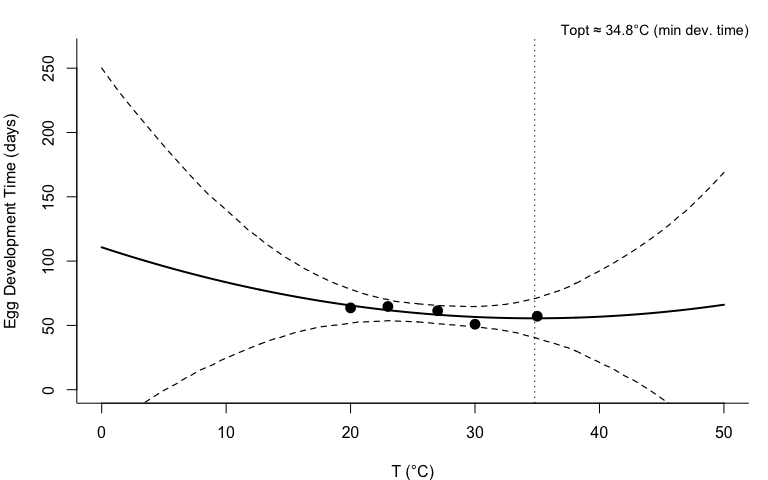

Egg Development Time (EDT)

**Fitted Quadratic Model (EDT):**

• Intercept = 58.23 

• Linear coefficient = -0.7303 

• Quadratic coefficient = 0.047594 

• Residual SD = 5.29 

• R-squared = 0.56 

**Model:** EDT = 58.23 + -0.7303 *(T - 27 ) + 0.047594 *(T - 27 )²

**Note:** Egg development time varies with temperature following quadratic relationship.

Pupal Development Time (PuDT)

**Fitted Quadratic Model (PuDT):**

• Intercept = 48.26 

• Linear coefficient = -3.6431 

• Quadratic coefficient = 0.307141 

• Residual SD = 2.48 

• R-squared = 0.993 

**Model:** PuDT = 48.26 + -3.6431 *(T - 27 ) + 0.307141 *(T - 27 )²

**Note:** Pupal development time decreases with temperature (faster development at higher T).